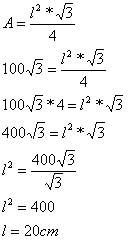Matemática & CIA: Exercícios

Exercícios Resolvidos

1) O valor positivo de x que torna a sucessão $formdata=\left(\frac+12,\,\,\,x,\,\,\,\frac+98\right)$ uma PG é
    (A) $formdata=\frac{1}{2}$
    (B) $formdata=\frac+14$
    (C) $formdata=\frac+32$
    (D) $formdata=\frac+34$
    (E) $formdata=\frac+38$

- Vamos usar a propriedade fundamental de uma PG para calcular o valor de "x".
$formdata=\frac{\,\,x\,\,}{\frac{1}{2}}=\frac{\frac{9}{8}}{\,\,x\,\,}$
$formdata=2x=\frac{9}{8x}$
$formdata=16x^2=9$
$formdata=x^2=\frac{9}{16}$
$formdata=x=\pm\sqrt{\frac{9}{16}}$
$formdata=x=\pm\frac{3}{4}$ Como o exercício pede só o valor positivo, a resposta é letra "D".

2) (UFRGS) Numa PG de razão positiva, o primeiro termo é igual ao dobro da razão, e a soma dos dois primeiros é 24. Nessa progressão a razão é
    (A) 1
    (B) 2
    (C) 3
    (D) 4
    (E) 5

- As informações do problema são:
    a₁=2q    S₂=24     q=?
- Sabemos que S₂=a₁+a₂ e iremos trabalhar em cima disto. Usando a fórmula do termo geral para o segundo termo, temos:
    a₂=a₁·q   Vamos substituir o valor de a₁ por 2q.
    a₂=2q·q
    a₂=2q²
- Voltando à nossa fórmula de trabalho:
    S₂=a₁+a₂     Vamos substituir os valores conhecidos
    24=2q+2q²
    2q+2q²-24=0    Chegamos numa equação do segundo grau, usando Bhaskara:
    q'=3    q''=-4      Como o exercício diz que a razão é positiva,
                               Resposta certa, letra "C".

3) O valor de x para que a seqüência $formdata=(x+1,\,\,x,\,\,x+2)$ seja uma PG é
    (A) $formdata=\frac+12$
    (B) $formdata=\frac+23$
    (C) $formdata=-\frac+23$
    (D) $formdata=-\frac+12$
    (E) $formdata=3$

- Novamente iremos utilizar a propriedade fundamental de uma PG:
$formdata=\frac{x}{x+1}=\frac{x+2}{x}$
- Desenvolvendo esta equação:
$formdata=x^2=(x+2)(x+1)\\x^2=x^2+3x+2\\0=3x+2\\3x=-2\\x=-\frac{2}{3}$ Resposta certa, letra "C".

4) O conjunto solução da equação $formdata=x+\frac+x3+\frac+x9+...=30$ é
    (A) 10
    (B) 15
    (C) 20
    (D) 25
    (E) 30

- Note que o lado esquerdo da igualdade é uma PG, com a₁=x e q=1/3. Como todos os termos estão sendo somados, temos uma soma infinita desta PG. Vamos utilizar a fórmula de soma infinita:
$formdata=S_n=\frac{a_1}{1-q}$
$formdata=S_n=\frac{x}{1-\frac+13}$
$formdata=S_n=\frac{\,\,x\,\,}{\frac+23}$
$formdata=S_n=\frac{3x}{2}$
- Vamos voltar a equação do exercício e substituir o valor recém calculado:
$formdata=x+\frac+x3+\frac+x9+...=30\\\frac{3x}2=30\\3x=60\\x=\frac{60}3=20$ Resposta certa, letra "C".

5) A soma dos termos de uma PG é expressa por $formdata=S_n=-3+3^{n+1}$ . A razão da progressão é
    (A) $formdata=2$
    (B) $formdata=3$
    (C) $formdata=6$
    (D) $formdata=sqrt+2$
    (E) $formdata=sqrt+6$

- O exercício dá a fórmula geral das soma dos "n" primeiros termos e pede sua razão. Para calcular a razão devemos calcular a₁ e a₂ para dividirmos e descobrir sua razão.
- Se substituirmos o valor de "n" por 1, iremos calcular a soma dos 1 primeiros termos, ou seja, o próprio primeiro termo:
    S₁= -3+3¹⁺¹
    S₁= -3+3²
    S₁= -3+9
    S₁= 6
    a₁=6
- Se substituirmos "n" por 2, iremos calcular a soma dos 2 primeiros termos, ou seja, a₁+a₂.
    S₂= -3+3²⁺¹
    S₂= -3+3³
    S₂= -3+27
    S₂= 24
- Substituino o que vale S₂, temos:
    S₂= 24
   a₁+a₂=24
    6+a₂=24
    a₂=24-6
    a₂=18
- Agora dividindo o segundo pelo primeiro termo temos a razão:
    $formdata=q=\frac{a_2}{a_1}\\q=\frac{18}{6}\\q=3$      Resposta certa, letra "B".

6) A soma de três números que formam uma PG crescente é 19 e, se subtrairmos 1 do primeiro, sem alterar os outros dois, eles passam a constituir uma PA. A diferença entre a soma dos dois primeiros números e o terceiro é:
    (A) -2
    (B) -1
    (C) 0
    (D) 1
    (E) 2

- Informações
PG={a₁,a₂,a₃} a₁+a₂+a₃=19
PA={(a₁-1),a₂,a₃}
- Agora com estas três informações conseguimos estruturar três equações e formar um sisteminha. Com a propriedade fundamental de uma PG tiramos a seguinte equação:

$formdata=\frac{a_2}{a_1}=\frac{a_3}{a_2}$

- Com a propriedade fundamental de uma PA tiramos a próxima equação:

$formdata=a_2-(a_1-1)=a_3-a_2$

- E a terceira equação já é dada, a₁+a₂+a₃=19. Formando o sistema:

$formdata=\left{\frac{a_2}{a_1}=\frac{a_3}{a_2}\\a_2-(a_1-1)=a_3-a_2\\a_1+a_2+a_3=19\right.$

- Um sistema de três equações é um pouco mais demorado de se resolver, mas vamos lá! Primeiro vamos isolar o valor de a₁ na terceira equação e substituir na segunda:

a₁=19-a₂-a₃	Agora vamos substituir este valor na segunda equação e ver no que dá.
a₂-(19-a₂-a₃-1)=a₃-a₂ a₂-19+a₂+a₃+1=a₃-a₂	Veja que podemos cortar os termos a₃ , pois temos ambos somando dos dois lados da equação
a₂-19+a₂+1=-a₂	Agora podemos calcular o valor de a₂. Vamos isolá-lo.
a₂+a₂+a₂=+19-1 3a₂=+18 a₂=18/3 a₂=6	Descobrimos o valor do a₂. Vamos voltar na primeira equação deste quadro e substituir o valor dele.
a₁=19-6-a₃ a₁=13-a₃	Temos a₁ em função de a₃, vamos substituir na primeira equção do sistema.
	Agora é só operar e calcular o valor de a₃.
36=a₃·(13-a₃) 36=13a₃-(a₃)² (a₃)²-13a₃+36=0	Caímos em uma equação do segundo grau de variável a₃, vamos aplicar Bhaskara.
$formdata=\frac{-(-13)\pm\sqrt{(-13)^2-4\cdot+4\cdot+1\cdot+36}}{2\cdot+1}\\\frac{13\pm\sqrt{25}}{2}\\\frac{13\pm+5}{2}=\left{\begin{array}{c}a_3'=9\\a_3''=4\end{array}\right.$	O problema diz que é uma PG crescente, portanto, se a₂=6 então o a₃ tem que ser maior que 6. Vale só a resposta a₃=9. Para calcular o a₁ voltamos à primeira equação deste quadro.
a₁=19-a₂-a₃ a₁=19-6-9 a₁=4	UFA, tá quase no fim. O exercício pede a diferença entre a soma dos dois primeiros números e o terceiro, portanto:
(a₁+a₂)-a₃ (4+6)-9 10-9 1	Resposta certa, letra "D"

7) A seqüência $formdata=(8x,\,5x-3,\,x+3,\,x)$ é uma progressão geométrica, de termos positivos, cuja razão é
    (A) $formdata=\frac+14$
    (B) $formdata=\frac+13$
    (C) $formdata=\frac+12$
    (D) $formdata=2$
    (E) $formdata=3$

- Nosso primeiro passo é achar o valor de "x", para depois substituir na progressão e achar a razão.
- Para calcular o "x" vamos usar a propriedade fundamental de uma PG:
    $formdata=\frac{5x-3}{8x}=\frac{x}{x+3}$
- Agora é só desenvolver e calcular o valor de "x".
    (5x-3)·(x+3)=x·8x
    5x²+15x-3x-9=8x²
    5x²-8x² +12x-9=0
    -3x²+12x-9=0    Chegamos em uma equação do segundo grau, aplicando Bhaskara:
    $formdata=\frac{-12\pm\sqrt{12^2-4\cdot(-3)\cdot(-9)}}{2\cdot(-3)}\\\frac{-12\pm\sqrt{36}}{-6}\\\frac{-2\pm+1}{-1}$ Com isso as nossa raízes são 1 e 3. Qual delas é a que vale? Se substituirmos na PG do exercício o x por 1 teremos uma sequência que não é uma PG. Portanto, o valor de x é 3.
- Sabendo o valor de "x" vamos substituir na PG e ver como ela é:
    (8x, 5x-3, x+3, x)
    (8·3, 5·3-3, 3+3, 3)
    (24, 12, 6, 3)    Esta é a PG
- Agora para achar a razão, dividimos o segundo pelo primeiro termo:
    $formdata=\frac{12}{24}=\frac+12$      Resposta certa, letra "C".

8) A soma dos termos da PG (5, 50, ..., 500000) é
    (A) 222 222
    (B) 333 333
    (C) 444 444
    (D) 555 555
    (E) 666 666

- Para podermos aplicar a fórmula da soma dos termos de uma PG, devemos saber qual ordem do número 500000 (tercerio, quarto, décimo...). Ou seja, devemos calcular o valor de "n".
- Informações:
    a₁=5    q=10    a_n=500000
- Vamos aplicar a fórmula do termo geral:
    a_n=a₁·q^(n-1)      Substituindo seus valores
    500000=5·10^(n-1)
    500000=5·10^(n-1)
    5·100000=5·10^(n-1)
    5·10⁵=5·10^(n-1)
    10⁵=10^(n-1) Agora podemos cortar as bases
    5=n-1
    n=6
- Agora sim, o termo 500000 é o sexto termo, podemos aplicar a fórmula da soma:
    $formdata=S_n=\frac{a_1\cdot(q^n-1)}{q-1}\\S_6=\frac{5\cdot(10^6-1)}{10-1}\\S_6=\frac{5\cdot(999999)}{9}\\S_6=5\cdot+111111\\S_6=555555$ Resposta certa, letra "D".

9) Ao interpolarmos 5 meios geométricos entre 1458 e 2, encontramos uma PG de razão:
    (A) $formdata=\pm\frac+12$
    (B) $formdata=\pm\frac+13$
    (C) $formdata=\pm\frac+14$
    (D) $formdata=\pm\frac+15$
    (E) $formdata=\pm\frac+16$

- Informações do problema:

1458 __ __ __ __ __ 2

a₁=1458 a₇=2 q=?
- Esta é a parte mais difícil do problema, ver que o 2 é o sétimo termo. Agora é só aplicar a fórmula do termo geral para o a₇.
$formdata=a_7=a_1\cdot+q^{(7-1)}\\2=1458\cdot+q^6\\q^6=\frac{2}{1258}=\frac{1}{729}\\q^6=\left(\frac{1}{3}\right)^6\\q=\pm\frac+13$ Como é um expoente PAR, ao "passa-lo" para o outro lado como raiz, deve-se incluir o sinal de ±. Resposta certa letra "B".

10) A razão de uma PG cujo termo geral é $formdata=a_n=2\cdot\sqrt{2^{n-3}}$ é
    (A) $formdata=sqrt+2$
    (B) $formdata=\frac{sqrt+2}{3}$
    (C) $formdata=\frac{3\sqrt+2}{2}$
    (D) $formdata=2\sqrt+2$
    (E) $formdata=4\sqrt+2$

- Para calcular-mos a razão, devemos saber no mínimo o primeiro e o segundo termo. Substituindo n por 1 e por 2 na fórmula do termo geral dada, temos:

$formdata=a_1=2\cdot\sqrt{2^{1-3}}\\a_1=2\cdot\sqrt{2^{-2}}\\a_1=2\cdot\sqrt{\frac{1}{4}}\\a_1=2\cdot\frac{1}{2}\\a_1=1$

$formdata=a_2=2\cdot\sqrt{2^{2-3}}\\a_2=2\cdot\sqrt{2^{-1}}\\a_2=2\cdot\sqrt{\frac{1}{2}}\\a_2=\frac{2}{sqrt+2}\\a_2=\frac{2}{\sqrt+2}\cdot\frac{sqrt+2}{sqrt+2}=sqrt+2$

- Agora, já sabendo a₁ e a₂, podemos calcular a razão:
$formdata=q=\frac{a_2}{a_1}\\q=\frac{sqrt+2}{1}\\q=sqrt+2$ Resposta certa, letra "A".

11) (PUC) De acordo com a disposição dos números abaixo,

A soma dos elementos da décima linha vale:

    (A) 2066
    (B) 5130
    (C) 10330
    (D) 20570
    (E) 20660

- Questão muito bem elaborada! Note que cada linha desta "pirâmide" é uma PA de razão 2. Cada linha tem um elemento a mais do que a linha anterior, sendo que sua ordem é igual ao número de termos (a segunda tem 2 termos a quinta tem 5 termos a décima tem 10 termos).
Veja também que a primeira coluna (que determina o primeiro elemento de cada linha) segue como uma PG de razão 2 e a₁=2. Então, o primeiro termo da décima linha será (a₁₀):

a₁₀=a₁·q⁹
a₁₀=2·2⁹
a₁₀=1024

- A décima linha será uma PA com a₁=1024 r=2 e terá 10 termos. Antes de calcularmos a soma (que o exercício pede) devemos calcular o valor do décimo termo desta PA:

a₁₀=a₁+9·r
a₁₀=1024+9·2
a₁₀=1024+18
a₁₀=1042

- Portanto, a soma dos termos (de acordo com a fórmula):
S₁₀=(a₁+a₁₀)·10/2
S₁₀=(1024+1042)·5
S₁₀=(2066)·5
S₁₀=10330 Resposta certa, letra "C".

Exercícios Resolvidos

Sabendo que o primeiro termo de uma PA é 5 e a razão é 11, calcule o 13^o termo:

- Primeiro devemos coletar todas informações do problema:
a₁=5 r=11 a₁₃=?
- Para calcular vamos utilizar a fórmula do termo geral, onde a_n será o a₁₃, portanto n=13. Agora, substituindo:

        a₁₃ = 5 + (13 - 1).11
        a₁₃ = 5 + (12).11
        a₁₃ = 5 + 132
        a₁₃ = 137

2) Dados a₅ = 100 e r = 10, calcule o primeiro termo:

        a₅ = a₁ + (5 - 1).r
        100 = a₁ + (5 - 1).10
        100 = a₁ + 40
        100 - 40 = a₁
        a₁ = 60

3) Sendo a₇ = 21 e a₉ = 27, calcule o valor da razão:

a₇ = a₁ + (7 - 1).r	Substituindo pelos valores	21 = a₁ + 6r
a₉ = a₁ + (9 - 1).r	Substituindo pelos valores	27 = a₁ + 8r

Note que temos duas incógnitas (a₁ e r) e duas equações, ou seja, temos um sistema de equações. Vamos isolar o a₁ na primeira equação e substituir na segunda:

a₁ = 21 - 6r

Agora, substituindo na segunda:

        27 = (21 - 6r) + 8r
        27 = 21 + 2r
        27 - 21 = 2r
        6 = 2r
        6/2 = r
        r = 3

4) (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:

        (A) 8^a
        (B) 7^a
        (C) 6^a
        (D) 5^a
        (E) 4^a

- informações do problema:
a₁ = 23 r = -6 a_n = -13 n=?

        - Substituindo na fórmula do termo geral:
        a_n = a₁ + (n-1)r
        -13 = 23 + (n - 1).(-6)
        -13 - 23 = -6n + 6
        -36 - 6 = -6n
        -42 = -6n      Vamos multiplicar os dois lados por (-1)
        6n = 42
        n = 42/6
        n = 7            Resposta certa letra "B

5) (UCS) O valor de x para que a seqüência (2x, x+1, 3x) seja uma PA é:

        (A) 1/2
        (B) 2/3
        (C) 3
        (D) 1/2
        (E) 2

- Informações:

          a₁= 2x
          a₂= x+1
          a₃= 3x

- Neste exercício devemos utilizar a propriedade de uma PA qualquer. Sabemos que o termo da frente é igual ao termo de trás mais a razão. Ou seja:

a₂ = a₁ + r	isolando "r"	r = a₂ - a₁
a₃ = a₂ + r	isolando "r"	r = a₃ - a₂

- Como temos "r" igualado nas duas equações, podes igualar uma a outra, ou seja:

a₂ - a_{1 =}a₃ - a₂

- Agora, substituindo pelos valores dados no enunciado:

        (x + 1) - (2x) = (3x) - (x + 1)
        x + 1 - 2x = 3x - x - 1
        x - 2x - 3x + x= -1 - 1
        -3x = -2             Multiplicando ambos os lados por (-1)
        3x = 2
        x = 2/3             Resposta certa letra "B"

Exercícios Resolvidos

Através de alguns exemplos iremos demonstrar as formas de resolução utilizando as fórmulas das progressões aritméticas e geométricas.

Exemplo 1

Seja (a₁, a₂, a₃, ... , an, ... , a₅₀) uma progressão aritmética. Se a₂ = 14, a₅ – a₃ = 18 e an = 239, então k é igual a:

Resolução:
Retirando os dados do problema temos:

a₂ = 14
a₅ – a₃ = 18
an = 239
n = ?
Para o cálculo de k devemos utilizar a equação an= a₁ + (n – 1) * r , mas para darmos continuidade devemos achar o valor de a1 e de r, observe os cálculos abaixo:

Utilizando o termo geral da P.A, an = a₁ + (n –1) . r podemos dizer que:
a₂ = a₁ + r
14 = a₁ + r

Utilizando novamente o termo geral da P.A, podemos dizer que:
a₅ = a₁+ 4r e a₃ = a₁ + 2r

Substituindo na situação do problema a₅ – a₃ = 18, temos:

a₁ + 4r – a₁ – 2r = 18 → unindo os termos semelhantes.

a₁ – a₁ + 4r – 2r = 18 → reduzindo os termos semelhantes.

2r = 18

r = 18/2

r = 9

Agora devemos descobrir o valor de a1, para isso substituiremos o valor de r = 9 na equação 14 = a₁ + r:

a₁ + 9 = 14

a₁ = 14 – 9

a₁ = 5

Agora que sabemos que a₁ = 5 e r = 9, podemos calcular qual é o termo n:

an = a₁ + (n – 1) * r → Substituído os dados na equação.

239 = 5 + (n – 1) * 9

239 = 5 + 9n – 9 → unindo os termos semelhantes.

239 – 5 + 9 = 9n
243 = 9n

n = 243/9

n = 27

Assim, descobrimos que an é o vigésimo sétimo termo da P.A.

Exemplo 2

Uma P.G de razão 3 foi formada introduzindo-se três termos entre o 2º termo e 486. Qual o 1º termo da P.G?

Resolução:

q = 3
Como foram introduzidos três termos entre o 2º termo e 486 podemos então concluir que 486 é o sexto termo da P.G.

a₁ , a₂, a₃, a₄, a₅, 486

a₃ , a₄ e a₅ são os três termos introduzidos.

Então podemos dizer que a₆ = 486, utilizando o termo geral de uma P.G
an = a₁ * q^{n – 1}, temos:

a₆ = a₁ * q^{n – 1} → Substituindo os dados.

486 = a₁ * 3 ^{6 – 1}

486 = a₁ * 3 ⁵

486 = a₁ * 243

a₁ = 486/243

a₁ = 2

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Exercícios Geometria Plana

Exemplo 1

Determine a medida da área de uma região triangular equilátera, com lados medindo 12 metros de comprimento.

A região triangular possui área medindo 36√3 metros.

Exemplo 2

Qual a medida da lateral de um triângulo equilátero que possui área total medindo 100√3 cm²?

Matemática & CIA

Páginas

Ache no Blog -->

Exercícios

Exercícios Resolvidos

Exercícios Resolvidos

Exercícios Resolvidos