Área e Volume Corpos Esféricos
Os corpos esféricos possuem enorme importância no cotidiano de diversas atividades. Em alguns esportes, o formato esférico é representado pela bola, que é o principal objeto no andamento das disputas de futebol, vôlei, basquete, boliche, golfe, entre outras modalidades esportivas. Nos objetos móveis como bicicletas, carros e caminhões, o formato esférico está presente em componentes mecânicos responsáveis pela locomoção de tais veículos. Nesses veículos, os rolamentos são formados por esferas que permitem que ocorra o giro de uma roda em um eixo. Veja figura representativa de um rolamento:

Os rolamentos também são muito utilizados no setor industrial, facilitando o trabalho de locomoção das partes de máquinas. Para analisarmos como objetos simples utilizam a característica dos corpos esféricos, podemos tomar como exemplo um frasco de desodorante Roll On. Nesses frascos, a transferência do líquido para a pele ocorre por meio de um movimento realizado por uma esfera.

Devido a essas inúmeras utilizações, a esfera possui, de acordo com a Matemática, no que diz respeito à Geometria Espacial, Área e Volume que são determinados por expressões algébricas matemáticas. Veja:
Área
Volume

Os cálculos matemáticos, envolvendo área e volume de uma esfera, abrangem a medida do raio que é a distância entre o centro da esfera e sua extremidade e o valor constante do número irracional π (pi), dado por aproximadamente 3,14. Veja a esfera e seus elementos:

Exemplo 1
Uma esfera de plástico possui raio medindo 20 centímetros. Determine a área dessa região esférica.

Exemplo 2
Um reservatório possui a forma esférica com 15 metros de raio. Calcule a capacidade total de armazenamento desse reservatório.

Temos que 1 m³ corresponde a 1000 litros. Então 942 m³ equivalem a 942 000 litros de capacidade de armazenamento.
Graduado em Matemática
Equipe Brasil Escola
Cone :
Ao estudarmos Geometria nos deparamos com várias situações geométricas, alguns sólidos possuem origem e fundamentos na sua formação, um deles é o cone, figura presente no cotidiano.
Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por segmentos de reta unindo o ponto P aos pontos do círculo.
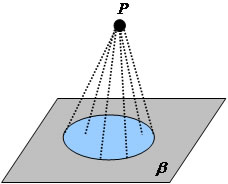
Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por segmentos de reta unindo o ponto P aos pontos do círculo.

Outra forma de construir o cone é através da revolução do triângulo retângulo sobre um eixo vertical.
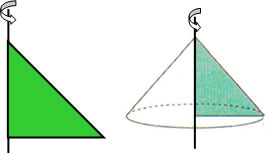

Elementos do cone
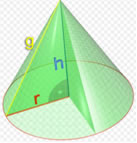
g: geratriz do cone
h: altura do cone
r: raio da base
v: vértice
Classificação do cone
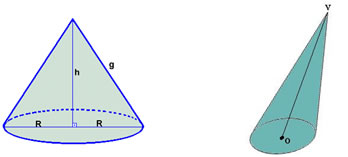
Cone reto Cone oblíquo

g: geratriz do cone
h: altura do cone
r: raio da base
v: vértice
Classificação do cone

Cone reto Cone oblíquo
No cone reto podemos aplicar a relação de Pitágoras para o cálculo da geratriz (g), do raio da base (r) e da altura (h), pois vimos que o cone pode ser formado através da revolução do triângulo retângulo. Comparando os elementos do cone aos do triângulo retângulo temos:
Geratriz no cone, hipotenusa no triângulo.
Altura no cone, cateto no triângulo.
Raio da base no cone, cateto no triângulo.
Uma importante relação no cone é dada por: r² + h² = g², observe a figura:
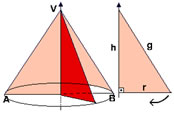
Áreas no cone
Área da base
Por ser uma circunferência, a área da base de um cone é dada pela seguinte expressão:
Área da lateral
A área lateral do cone é dada pela seguinte expressão:
Área total
É dada somando-se a área lateral e a área da base.
At = Al + Ab
At = Πr(g+r)
Volume do cone
O volume do cone é dado pelo produto da área da base pela altura divido por três.
V = (Πr²h)/3

Planificação do cone
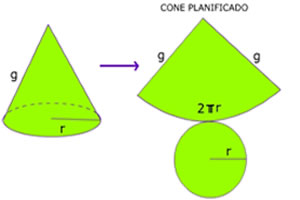
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Graduado em Matemática
Equipe Brasil Escola
Cilindro :
Cilindro Circular
Sejam α e β dois planos paralelos distintos, uma reta s secante a esses planos e um círculo C de centro O contido em α. Consideremos todos os segmentos de reta, paralelos a s, de modo que cada um deles tenha um extremo pertencente ao círculo C e o outro extremo pertencente a β.

Sejam α e β dois planos paralelos distintos, uma reta s secante a esses planos e um círculo C de centro O contido em α. Consideremos todos os segmentos de reta, paralelos a s, de modo que cada um deles tenha um extremo pertencente ao círculo C e o outro extremo pertencente a β.

A reunião de todos esses segmentos de reta é um sólido chamado de cilindro circular, limitado de bases C e C’ ou simplesmente cilindro circular.
Cilindro circular reto
No cilindro circular reto a geratriz forma com o plano da base um ângulo de 90º. No cilindro circular reto a medida h de uma geratriz é a altura do cilindro.
Cilindro circular reto
No cilindro circular reto a geratriz forma com o plano da base um ângulo de 90º. No cilindro circular reto a medida h de uma geratriz é a altura do cilindro.

O cilindro circular reto também é conhecido por cilindro de revolução, pois pode ser obtido pela revolução de 360º de uma região retangular em torno de um eixo.

Cilindro equilátero
O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero.
No cilindro equilátero a altura é igual ao diâmetro da base: h = 2r.

O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero.
No cilindro equilátero a altura é igual ao diâmetro da base: h = 2r.

Área Lateral e Área total de um cilindro circular reto
A superfície de um cilindro reto de altura h e raio da base r é equivalente à reunião de uma região retangular, de lados 2πr e h, com dois círculos de raio r. Observe a planificação do cilindro.

A superfície de um cilindro reto de altura h e raio da base r é equivalente à reunião de uma região retangular, de lados 2πr e h, com dois círculos de raio r. Observe a planificação do cilindro.

A área do retângulo equivalente à superfície lateral do cilindro é a área lateral Aℓ do cilindro, ou seja:
Aℓ = 2*π*r*h
A área total At do cilindro é igual à soma da área lateral Aℓ com as áreas das duas bases, ou seja:
At = 2*π*r*h + π*r2 + π*r2 → At = 2*π*r*h + 2π*r2
Volume do cilindro circular
O volume V de um cilindro circular de altura h e raio da base r é igual ao produto da área da base, πr2, pela altura h, isto é:
V = π*r2*h
Aℓ = 2*π*r*h
A área total At do cilindro é igual à soma da área lateral Aℓ com as áreas das duas bases, ou seja:
At = 2*π*r*h + π*r2 + π*r2 → At = 2*π*r*h + 2π*r2
Volume do cilindro circular
O volume V de um cilindro circular de altura h e raio da base r é igual ao produto da área da base, πr2, pela altura h, isto é:
V = π*r2*h
Esfera:
A esfera é obtida através da revolução da semicircunferência sobre um eixo. Podemos considerar que a esfera é um sólido.


Alguns conceitos básicos estão relacionados à esfera, se considerarmos a superfície esférica destacamos os seguintes elementos básicos:
Pólos
Equador
Paralelo
Meridiano

Pólos
Equador
Paralelo
Meridiano

Área de uma superfície esférica
Temos que a área de uma superfície esférica de raio r é igual a:

Volume da esfera
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:

Temos que a área de uma superfície esférica de raio r é igual a:
Volume da esfera
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:

Posição relativa entre plano e esfera
Plano secante à esfera
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.
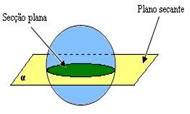
Plano tangente à esfera
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.
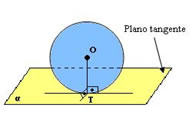
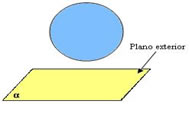
Plano externo à esfera
O plano e a esfera não possuem pontos em comum.
Plano secante à esfera
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.

Plano tangente à esfera
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.

Plano externo à esfera
O plano e a esfera não possuem pontos em comum.

A esfera possui inúmeras aplicações, como exemplo podemos citar a Óptica (Física), a seção de uma esfera forma uma lente esférica, que são objetos importantes na construção de óculos. Corpos esféricos possuem grande importância na Engenharia Mecânica, a parte interior de inúmeras peças capazes de realizar movimentos circulares sobre eixos é constituída de esferas de aço. Um bom exemplo dessas peças é o rolamento.
Pirâmides:
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados do polígono da base.

Os segmentos AV, BV e CV são as arestas laterais da pirâmide.
Os pontos A, B, C e V são os vértices.
Os triângulos VAB,VBC e VCA são as faces laterais.
O triângulo ABC é outra face da pirâmide e constitui a base.
A distância do ponto V ao centro da base constitui a altura da pirâmide.
A classificação de uma pirâmide depende do número de arestas da região da área da base.
Base é um triângulo
Nome: pirâmide triangular
Número de faces: três faces laterais mais face da base, portanto, quatro faces.
Base é um quadrado
Nome: pirâmide quadrangular
Número de faces: quatro faces laterais mais face da base, portanto, cinco faces.
Base é um pentágono
Nome: pirâmide pentagonal
Número de faces: cinco faces laterais mais face da base, portanto, seis faces.
Base é um hexágono
Nome: pirâmide de base hexagonal
Número de faces: seis faces laterais mais face da base, portanto, sete faces.

Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
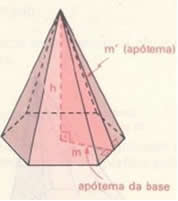
Altura, apótema da base e apótema da pirâmide
h: altura da pirâmide
m’: apótema da pirâmide
m: apótema da base
Pelo teorema de Pitágoras temos:
m’² = h² + m²
Área da base
A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:

onde P: perímetro do polígono e a: apótema do polígono.
Área lateral
É a soma de todas as áreas laterais.
Área total
Soma da área lateral com a área da base.
At = Al + Ab
Volume
O volume de uma pirâmide é dado pela expressão:

onde Ab: área da base (depende do polígono) e h: altura da pirâmide.
Planificação de uma pirâmide
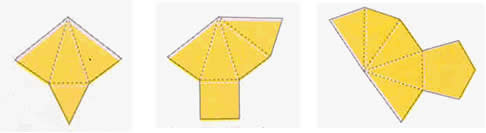
Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal

Os segmentos AV, BV e CV são as arestas laterais da pirâmide.
Os pontos A, B, C e V são os vértices.
Os triângulos VAB,VBC e VCA são as faces laterais.
O triângulo ABC é outra face da pirâmide e constitui a base.
A distância do ponto V ao centro da base constitui a altura da pirâmide.
A classificação de uma pirâmide depende do número de arestas da região da área da base.
Base é um triângulo
Nome: pirâmide triangular
Número de faces: três faces laterais mais face da base, portanto, quatro faces.
Base é um quadrado
Nome: pirâmide quadrangular
Número de faces: quatro faces laterais mais face da base, portanto, cinco faces.
Base é um pentágono
Nome: pirâmide pentagonal
Número de faces: cinco faces laterais mais face da base, portanto, seis faces.
Base é um hexágono
Nome: pirâmide de base hexagonal
Número de faces: seis faces laterais mais face da base, portanto, sete faces.

Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
Altura, apótema da base e apótema da pirâmide
h: altura da pirâmide
m’: apótema da pirâmide
m: apótema da base
Pelo teorema de Pitágoras temos:
m’² = h² + m²

Área da base
A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:
onde P: perímetro do polígono e a: apótema do polígono.
Área lateral
É a soma de todas as áreas laterais.
Área total
Soma da área lateral com a área da base.
At = Al + Ab
Volume
O volume de uma pirâmide é dado pela expressão:
onde Ab: área da base (depende do polígono) e h: altura da pirâmide.
Planificação de uma pirâmide

Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
Poliedros:
As figuras geométricas espaciais também recebem o nome de sólidos geométricos, que são divididos em: poliedros e corpos redondos. Vamos abordar as definições e propriedades dos poliedros.
Poliedros são figuras geométricas formadas por três elementos básicos: vértices, arestas e faces. Um poliedro é considerado regular quando suas faces são polígonos regulares e congruentes.
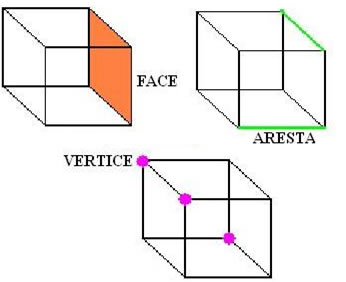
Dentre os poliedros existentes, existem alguns considerados Poliedros de Platão, pois todas as faces possuem o mesmo número de arestas, todos os ângulos poliédricos possuem o mesmo número de arestas e se enquadram na relação de Euler. Os Poliedros considerados de Platão são:
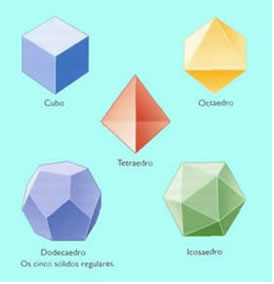
Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.
A fórmula de Euler está atribuída à relação de dependência entre os elementos de um poliedro. A expressão matemática desenvolvida por Leonhard Euler, matemático suíço, é a seguinte: V – A + F = 2. Onde:
V = vértice
A = arestas
F = Faces
Essa expressão determina o número de faces, arestas e vértices de qualquer poliedro.
Por volta do século VI antes de Cristo, o filósofo Platão estudou os poliedros platônicos relacionando-os aos elementos da natureza. Veja a associação feita por ele:
Tetraedro: fogo
Hexaedro (cubo): terra
Octaedro: ar
Icosaedro: água
Dodecaedro: universo
Além dos poliedros de Platão, os sólidos geométricos como: prismas, pirâmides, paralelepípedos, blocos retangulares e quadrangulares são considerados poliedros.
Poliedros são figuras geométricas formadas por três elementos básicos: vértices, arestas e faces. Um poliedro é considerado regular quando suas faces são polígonos regulares e congruentes.

Dentre os poliedros existentes, existem alguns considerados Poliedros de Platão, pois todas as faces possuem o mesmo número de arestas, todos os ângulos poliédricos possuem o mesmo número de arestas e se enquadram na relação de Euler. Os Poliedros considerados de Platão são:

Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.
A fórmula de Euler está atribuída à relação de dependência entre os elementos de um poliedro. A expressão matemática desenvolvida por Leonhard Euler, matemático suíço, é a seguinte: V – A + F = 2. Onde:
V = vértice
A = arestas
F = Faces
Essa expressão determina o número de faces, arestas e vértices de qualquer poliedro.
Por volta do século VI antes de Cristo, o filósofo Platão estudou os poliedros platônicos relacionando-os aos elementos da natureza. Veja a associação feita por ele:
Tetraedro: fogo
Hexaedro (cubo): terra
Octaedro: ar
Icosaedro: água
Dodecaedro: universo
Além dos poliedros de Platão, os sólidos geométricos como: prismas, pirâmides, paralelepípedos, blocos retangulares e quadrangulares são considerados poliedros.
Prisma:
Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas características básicas definem esse sólido geométrico. Por exemplo, o número de faces do prisma será exatamente igual ao número de lados do polígono que constitui suas bases (superior e inferior), dessa forma, sua classificação quanto ao número de lados pode ser:
Triangular – base constituída de triângulos.
Quadrangular – base constituída de quadriláteros.
Pentagonal – base constituída de pentágonos.
Hexagonal – base constituída de hexágonos.
Heptagonal – base constituída de heptágonos.
Octogonal – base constituída de octógonos.
Os prismas também podem ser classificados como retos ou oblíquos. Os prismas retos são aqueles em que a aresta lateral forma com a base um ângulo de 90º, os oblíquos são aqueles em que as arestas formam ângulos diferentes de 90º.
Triangular – base constituída de triângulos.
Quadrangular – base constituída de quadriláteros.
Pentagonal – base constituída de pentágonos.
Hexagonal – base constituída de hexágonos.
Heptagonal – base constituída de heptágonos.
Octogonal – base constituída de octógonos.
Os prismas também podem ser classificados como retos ou oblíquos. Os prismas retos são aqueles em que a aresta lateral forma com a base um ângulo de 90º, os oblíquos são aqueles em que as arestas formam ângulos diferentes de 90º.
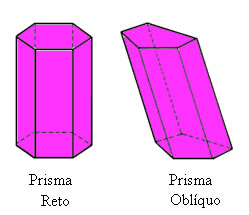
Todos os prismas possuem área da base, área lateral, área total e volume. Todas essas medidas dependem do formato do polígono que se encontra nas bases; por exemplo, os prismas acima possuem em sua base um pentágono, portanto, para calcularmos a área dessa base devemos determinar a área do pentágono. No caso do prisma pentagonal reto, as faces laterais constituem retângulos e a do prisma oblíquo é formada por paralelogramos.
A área total de um prisma é calculada somando a área lateral e o dobro da área da base. E o volume é determinado calculando a área da base multiplicada pela medida da altura.
Observe alguns exemplos de prismas:
Prisma Triangular Reto
A área total de um prisma é calculada somando a área lateral e o dobro da área da base. E o volume é determinado calculando a área da base multiplicada pela medida da altura.
Observe alguns exemplos de prismas:
Prisma Triangular Reto
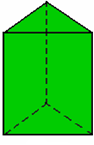
Prisma Hexagonal Reto
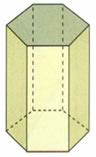
Prisma Pentagonal Oblíquo

Prisma Quadrangular Oblíquo
Cilindro:
O cilindro, como todo sólido geométrico, possui um volume que determina a sua capacidade. Todo cilindro possui uma base no formato de circunferência de raio r e uma altura h. Seu volume é dado através da multiplicação entre a área da base no formato circular e a medida da altura h. Observe:
Área da base circular → Ab = π * r²
Volume
V = Ab * h → V = π * r² * h
Esse tipo de sólido geométrico é muito utilizado no cotidiano como reservatório de substâncias liquidas e gasosas.
Quando trabalhamos com sólidos geométricos precisamos relembrar as principais relações entre as medidas de volume e de capacidade, veja:
1 m³ (metro cúbico) = 1 000 litro
1 dm³ (decímetro cúbico) = 1 litro
1 cm³ (centímetro cúbico) = 1 ml
Exemplo 1
Um tanque no formato cilíndrico é utilizado no armazenamento de combustível de uma transportadora de produtos alimentícios. As medidas desse tanque são as seguintes: raio da base medindo 4 metros e altura igual a 12 metros. Deseja-se encher esse tanque com óleo diesel para abastecer a frota de 150 caminhões que possuem o tanque também no formato cilíndrico, medindo 1,5 metros de altura e raio da base medindo 90 centímetros. Verifique se a quantidade de óleo diesel a ser armazenado no tanque da empresa é necessária para abastecer todos os caminhões uma única vez durante um dia, considerando que o combustível dos caminhões esteja bem próximo de acabar.
Volume do tanque da empresa
V = π * r² * h
V = 3,14 * 4² * 12
V = 3,14 * 16 * 12
V = 602,88 m³
Volume do tanque de cada caminhão
90 centímetros equivale a 0,9 metros
V = π * r² * h
V = 3,14 * 0,9² * 1,5
V = 3,14 * 0,81 * 1,5
V = 3,8151 m³
Quantidade necessária de combustível para abastecer a frota:
150 * 3,8151 = 572,27 m³
A capacidade total do tanque de armazenamento é de 602,88 m³ e a quantidade necessária para abastecer todos os caminhões é de 572,27 m³, então o óleo diesel do tanque é suficiente para abastecer toda a frota e ainda sobram 30,61 m³ de óleo.
Exemplo 2
Deseja-se construir um tanque no formato cilíndrico com volume de, aproximadamente, 250 m³ (metros cúbicos) e altura igual a 9 metros. Determine a medida aproximada do raio da base.
V = π * r² * h
250 = 3,14 * r² * 9
250 = 28,26 * r²
r² = 250 / 28,26
r² = 8,84
√r² = √8,84
r = 2,9 m (aproximadamente)
Área da base circular → Ab = π * r²
Volume
V = Ab * h → V = π * r² * h
Esse tipo de sólido geométrico é muito utilizado no cotidiano como reservatório de substâncias liquidas e gasosas.
Quando trabalhamos com sólidos geométricos precisamos relembrar as principais relações entre as medidas de volume e de capacidade, veja:
1 m³ (metro cúbico) = 1 000 litro
1 dm³ (decímetro cúbico) = 1 litro
1 cm³ (centímetro cúbico) = 1 ml
Exemplo 1
Um tanque no formato cilíndrico é utilizado no armazenamento de combustível de uma transportadora de produtos alimentícios. As medidas desse tanque são as seguintes: raio da base medindo 4 metros e altura igual a 12 metros. Deseja-se encher esse tanque com óleo diesel para abastecer a frota de 150 caminhões que possuem o tanque também no formato cilíndrico, medindo 1,5 metros de altura e raio da base medindo 90 centímetros. Verifique se a quantidade de óleo diesel a ser armazenado no tanque da empresa é necessária para abastecer todos os caminhões uma única vez durante um dia, considerando que o combustível dos caminhões esteja bem próximo de acabar.
Volume do tanque da empresa
V = π * r² * h
V = 3,14 * 4² * 12
V = 3,14 * 16 * 12
V = 602,88 m³
Volume do tanque de cada caminhão
90 centímetros equivale a 0,9 metros
V = π * r² * h
V = 3,14 * 0,9² * 1,5
V = 3,14 * 0,81 * 1,5
V = 3,8151 m³
Quantidade necessária de combustível para abastecer a frota:
150 * 3,8151 = 572,27 m³
A capacidade total do tanque de armazenamento é de 602,88 m³ e a quantidade necessária para abastecer todos os caminhões é de 572,27 m³, então o óleo diesel do tanque é suficiente para abastecer toda a frota e ainda sobram 30,61 m³ de óleo.
Exemplo 2
Deseja-se construir um tanque no formato cilíndrico com volume de, aproximadamente, 250 m³ (metros cúbicos) e altura igual a 9 metros. Determine a medida aproximada do raio da base.
V = π * r² * h
250 = 3,14 * r² * 9
250 = 28,26 * r²
r² = 250 / 28,26
r² = 8,84
√r² = √8,84
r = 2,9 m (aproximadamente)
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Graduado em Matemática
Equipe Brasil Escola
Nenhum comentário:
Postar um comentário